Introduction to designing variational algorithms in quantum computing

Variational algorithms have different parts that can be combined and improved with better algorithms, software, and hardware. They have 

• a cost function that explains a particular problem using certain values, 
• an ansatz to show the possible solutions using these values, and 
• an optimizer to keep trying different values until it finds the best solution. 

The optimizer checks the cost function with the current values and picks new values for the next try until it finds the best solution. These algorithms use both quantum and classical resources to work together. Hence we call those hybrid algorithms.

In this article, we will learn how to design a variational algorithm using qiskit.

First, we present an overview of the steps of developing a variational algorithm. This is a hybrid workflow because this involves both quantum and classical processing.

Overview of designing a variational algorithm

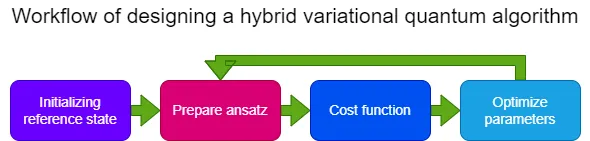
Step 1: Initialization Task 

Variational algorithms begin by setting up the quantum computer in a starting state $|0\rangle$. After that, they change it to a particular state $|\rho\rangle$, which is not described by parameters and is known as the reference state.

This change is achieved by applying a reference operator $U_R$, a special unitary operator, to the initial state. In a mathematical sense, this can be expressed as $U_R |0\rangle = |\rho\rangle$.

Step 2: Preparing the Ansatz 

To start optimizing from the initial state $|0\rangle$ to the desired state $|\psi(\vec{\theta})\rangle$, we need to create a variational form $U_V(\vec{\theta})$. This form represents a set of states with parameters that our algorithm will explore during optimization.

We call a specific combination of the reference state and the variational form an ansatz, denoted as $U_A(\vec{\theta}) := U_V(\vec{\theta})U_R$. Ansatz configurations will be represented by parametrized quantum circuits capable of transforming the initial state $|0\rangle$ into the target state $|\psi(\vec{\theta})\rangle$.

In summary, the process can be expressed mathematically as follows:

$\begin{aligned} |0\rangle \xrightarrow{U_R} U_R|0\rangle & = |\rho\rangle \xrightarrow{U_V(\vec{\theta})} U_A(\vec{\theta})|0\rangle \\[1mm] & = U_V(\vec{\theta})U_R|0\rangle \\[1mm] & = U_V(\vec{\theta})|\rho\rangle \\[1mm] & = |\psi(\vec{\theta})\rangle \\[1mm] \end{aligned}$

Step 3: Evaluating Cost Function

We can represent our problem using a cost function $C(\vec\theta)$, which is a combination of Pauli operators, implemented on a quantum system. This cost function may describe information about a physical system, like energy or spin. Additionally, we can encode non-physical problems. To handle noise and errors during the evaluation of our cost function, we can use Qiskit Runtime primitives for error suppression and mitigation.

Step 4: Optimizing Parameters 

The evaluations move to a classical computer, where a classical optimizer examines them and selects the next set of values for the variational parameters. If there is a known optimal solution, we can use it as the starting point $\vec\theta_0$ to kickstart our optimization. Starting with this initial state $|\psi(\vec\theta_0)\rangle$ may assist the optimizer in reaching a valid solution more quickly.

Step 5: Adjusting Ansatz Parameters with Results and Re-running 

The complete process is repeated until the classical optimizer meets its finalization criteria, and it provides an optimal set of parameter values $\vec\theta^*$. The suggested solution for our problem will then be $|\psi(\vec\theta^)\rangle = U_A(\vec\theta^*)|0\rangle$.

Variational Theorem 

A common objective of variational algorithms is to identify the quantum state with the lowest or highest eigenvalue of a specific observable. An essential concept we will utilize is the variational theorem of quantum mechanics. Before presenting its complete statement, let’s delve into some of the mathematical intuition behind it.

Mathematical Intuition for Energy and Ground States

In quantum mechanics, energy is represented by a quantum observable known as the Hamiltonian, denoted as $\hat{\mathcal{H}}$. Let’s consider its spectral decomposition:

$\hat{\mathcal{H}} = \sum_{k=0}^{N-1} \lambda_k |\phi_k\rangle \langle \phi_k|,$

where $N$ is the dimensionality of the space of states, $\lambda_{k}$ is the k-th eigenvalue or energy level, and $|\phi_k\rangle$ is the corresponding eigenstate: $\hat{\mathcal{H}}|\phi_k\rangle = \lambda_k |\phi_k\rangle$. For a system in the (normalized) state $|\psi\rangle$, the expected energy is given by:

$\begin{aligned}\langle \psi | \hat{\mathcal{H}} | \psi \rangle & = \langle \psi |\bigg(\sum_{k=0}^{N-1} \lambda_k |\phi_k\rangle \langle \phi_k|\bigg) | \psi \rangle \\& = \sum_{k=0}^{N-1} \lambda_k |\langle \psi |\phi_k\rangle|^2 \\& = \sum_{k=0}^{N-1} \lambda_k |\langle \psi |\phi_k\rangle|^2.\end{aligned}$

If we consider that $\lambda_0\leq \lambda_k$ for all $k$, then:

$\begin{aligned}\langle \psi | \hat{\mathcal{H}} | \psi \rangle & \geq \sum_{k=0}^{N-1} \lambda_0 |\langle \psi |\phi_k\rangle|^2 \\& = \lambda_0 \sum_{k=0}^{N-1} |\langle \psi |\phi_k\rangle|^2 \\& = \lambda_0.\end{aligned}$

Since $\{|\phi_k\rangle \}_{k=0}^{N-1}$ is an orthonormal basis, the probability of measuring $|\phi_{k} \rangle$ is $p_k = |\langle \psi |\phi_{k} \rangle |^2$, and the sum of all probabilities is such that $\sum_{k=0}^{N-1} |\langle \psi |\phi_k\rangle|^2 = \sum_{k=0}^{N-1}p_k = 1$. In summary, the expected energy of any system is higher than the lowest energy or ground state energy:

$\langle \psi | \hat{\mathcal{H}} | \psi \rangle \geq \lambda_0.$

This argument applies to any valid (normalized) quantum state $|\psi\rangle$, so we can consider parametrized states $|\psi(\vec\theta)\rangle$ that depend on a parameter vector $\vec\theta$. This is where the “variational” aspect comes into play. If we have a cost function $C(\vec\theta) := \langle \psi(\vec\theta)|\hat{\mathcal{H}}|\psi(\vec\theta)\rangle$ and want to minimize it, the minimum will always satisfy:

$\min_{\vec\theta} C(\vec\theta) = \min_{\vec\theta} \langle \psi(\vec\theta)|\hat{\mathcal{H}}|\psi(\vec\theta)\rangle \geq \lambda_0.$

The minimum value of $C(\vec\theta)$ will be the closest we can get to $\lambda_0$ using the parametrized states $|\psi(\vec\theta)\rangle$, and equality will only be reached if there exists a parameter vector $\vec\theta^*$ such that $|\psi(\vec\theta^*)\rangle = |\phi_0\rangle$.

Variational Theorem of Quantum Mechanics

If the (normalized) state $|\psi\rangle$ of a quantum system depends on a parameter vector $\vec\theta$, then the optimal approximation of the ground state (i.e., the eigenstate $|\phi_0\rangle$ with the minimum eigenvalue $\lambda_0$) is the one that minimizes the expectation value of the Hamiltonian $\hat{\mathcal{H}}$:

$\langle \hat{\mathcal{H}} \rangle(\vec\theta) := \langle \psi(\vec\theta) |\hat{\mathcal{H}}| \psi(\vec\theta) \rangle \geq \lambda_0.$

The reason why the variational theorem is stated in terms of energy minima is that it includes a number of mathematical assumptions:

1. For physical reasons, a finite lower bound to the energy $E \geq \lambda_0 > -\infty$ needs to exist, even for $N\rightarrow\infty$.

2. Upper bounds do not generally exist.

However, mathematically speaking, there is nothing special about the Hamiltonian $\hat{\mathcal{H}}$ beyond these assumptions, so the theorem can be generalized to other quantum observables and their eigenstates provided they follow the same constraints. Also, note that if finite upper bounds exist, the same mathematical arguments could be made for maximizing eigenvalues by swapping lower bounds for upper bounds.

Conclusion

Variational quantum algorithms epitomize the convergence of quantum and classical computing prowess, offering a potent approach to problem-solving. In this synthesis, cost functions illuminate the problem landscape, ansatz configurations provide potential solutions, and classical optimizers iteratively refine parameters, resulting in a dynamic interplay between quantum and classical resources. The journey through Qiskit’s hybrid workflow underscores the promise of variational algorithms, not just as mathematical constructs but as pragmatic tools with the potential to tackle complex challenges at the intersection of quantum and classical computing realms.

As we explore the variational theorem’s mathematical foundations, its application extends beyond the Hamiltonian, offering a versatile framework for optimizing ground states. The elegance of variational algorithms lies in their adaptability, and as quantum computing evolves, these algorithms stand poised to unlock new dimensions of computational capabilities, pushing the boundaries of what’s achievable in the quantum landscape.